Mapas Hexagonales (II) Coordenadas Hexagonales
Mapas Hexagonales (II): Coordenadas Hexagonales
En el artículo anterior realizamos una somera introducción al uso de mapas hexagonales en videojuegos. En esta entrada iniciamos la serie propiamente dedicada a la programación de mapas hexagonales. En concreto, el resto del artículo trata los siguientes temas:
- Propiedades del hexágono
- Coordenadas hexagonales
- Conversión de coordenadas hexagonales a píxeles
- Direccionalidad y cálculo de vecinos
- Conversión de píxeles a coordenadas hexagonales
Propiedades del hexágono
En geometría, un hexágono (o exágono) es un polígono de seis lados y seis vértices.
Propiedades generales
- Un hexágono tiene 9 diagonales
- La suma de todos los ángulos internos es 720º (4π radianes)
Hexágono regular
- Ángulos internos son congruentes midiendo 120° ó 2 π/3 radianes.
- Cada ángulo externo del hexágono regular mide 240° ó 4 π/3 radianes
-
Está íntimamente relacionado con los triángulos equiláteros:
- Uniendo cada vértice con su opuesto, el hexágono regular queda dividido en seis triángulos equiláteros.
- Numérense los vértices de 1 a 6 siguiendo las agujas del reloj. Uniendo los vértices impares se obtiene un triángulo equilátero; uniendo los vértices pares se obtiene otro.
- Se puede teselar el plano con hexágonos sin dejar ningún hueco. La siguiente imagen muestra un hexágono regular y las principales dones que nos interesan.
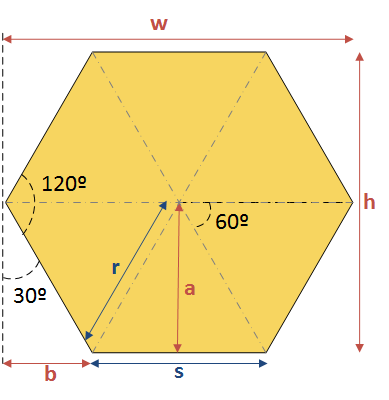
La principal magnitud a tener en cuenta es el lado s. Un hexágono regular se puede caracterizar completamente a partir del tamaño de su lado, o lo que es lo mismo, de su radio r, ya que son iguales. El resto de magnitudes se derivan de s y de los ángulos conocidos. Las otras magnitudes importantes que necesitamos para trabajar con mapas hexagonales son:
- La apotema a = s * Cos(30º)
- El segmento de longitud b = s * Sin(30º)** **
- La anchura del rectángulo_ w = 2 * b + s_
- La altura del rectángulo_ h _= 2 * a
Coordenadas hexagonales
En una retícula cuadrada, a la hora de escoger el sistema de coordenadas hay un sistema obvio: se usan 2 ejes ortogonales: filas y columnas. Ya que en informática gráfica se suele poner el origen de coordenadas en la esquina superior izquierda, parece lógico adoptar la misma convención a la hora de nombrar las coordenadas de una cuadrícula, así es mucho más fácil la conversión entre coordenadas del mapa y píxeles. Pero, ¿qué ocurre en una configuración hexagonal? Con una disposición hexagonal hay muchas más opciones. La opción que se suele emplear en los juegos de tablero intenta reproducir de la manera más aproximada posible el sistema usado en las retículas cuadradas, es decir con 2 ejes ortogonales. Cuando se utilizan hexágonos como teselas, hay diferentes formas de construir el teselado, pues los hexágonos se pueden colocar con 2 orientaciones diferentes (horizontal o vertical). Además, para cada orientación hay diferentes formas de establecer los límites o bordes del mapa. Si tratamos de dar al mapa una forma cuadrada o rectangular, entonces hay 2 formas de crear el límite, tal y como se muestra en la imagen siguiente.
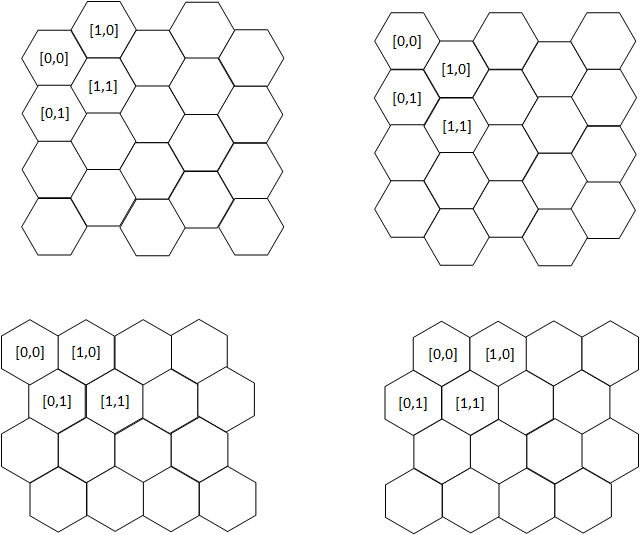
La primera fila muestra las 2 variantes con los hexágonos en disposición horizontal, mientras que la segunda fila hace lo propio con una disposición vertical. En total hay 4 variantes porque para cada orientación de los hexágonos hay 2 formas de asignar coordenadas a partir del origen. Nótese que con una disposición horizontal hay diferencias entre las columnas pares e impares; mientras que con una disposición vertical hay diferencias entre las filas pares e impares. Estas diferencias son fundamentales para desarrollar funciones que permitan pasar de coordenadas de mapa a píxeles de imagen y viceversa. A partir de ahora adoptaremos como referencia o modelo el primer caso: hexágonos horizontales, con las columnas impares más bajas que las pares. La siguiente imagen muestra en detalle las principales medidas a tener en cuenta para manipular gráficamente mapas de teselado hexagonal.
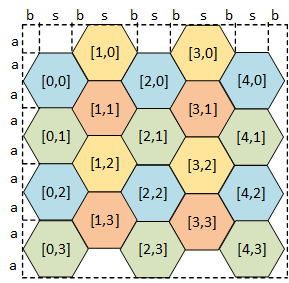
Como se puede ver, existe relación entre las coordenadas del mapa y las diferentes medidas del hexágono ( s, a y b), que ya hemos visto como se calculan.
Conversión de coordenadas hexagonales a píxeles
Rectángulo circunscrito
Para establecer una correspondencia entre coordenadas de mapa y coordenadas de imagen (píxeles) tenemos que considerar la forma de representar los hexágonos gráficamente. En general, para almacenar un gráfico en un archivo se utiliza una imagen de formato rectangular. Así pues, la opción sencilla para almacenar gráficos hexagonales es el uso de imágenes rectangulares con el tamaño del rectángulo circunscrito, ese que tiene como dimensiones w y h, (véase figura “Geometría del hexágono”). Para representar un gráfico hexagonal en un rectángulo tan solo es necesario definir la zona externa al hexágono como transparente mediante el uso de un canal alfa. La imagen siguiente muestra un gráfico hexagonal y su correspondiente rectángulo circunscrito; la zona pintada de rosa sería transparente (el rosa sería el canal alfa).
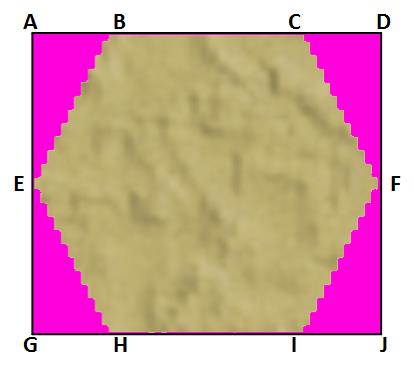
Cuando vayamos a pintar hexágonos sobre una pantalla, necesitaremos colocar su imagen en una determinada posición, que se corresponderá con las coordenadas de su vértice A, pues a partir de ese punto y conociendo s, a y b, es posible obtener los demás puntos.
Vamos a ver como se calcula A. Pero antes mostramos como quedan distribuidos los rectángulos contenedores de hexágonos en un mapa hexagonal.
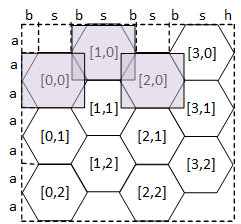
Si nos fijamos en la imagen anterior observaremos dos propiedades importantes:
- Que los rectangulos circunscritos a los hexágonos quedan solapados unos con otros
- Que la posición del vértice A es diferentes dependiendo de si estamos en una columna par o impar
Dadas las coordenadas <i,j> de un hexágono de nuestro mapa (i es la columna y j es la fila), vamos a calcular las coordenadas <x,y> del píxel correspondiente al punto A del rectángulo que contiene ese hexágono, como sigue:
x = i * (s + r)
SI (i es un número par)
ENTONCES y = a * j + r
SINO y = a * j'''La operación complementaria al cálculo anterior es la conversión de píxeles a coordenadas hexagonales. Para explicar esa conversión, es muy conveniente introducir antes la cuestión de las direcciones y el cálculo de los hexágonos vecinos a otro.

Direcciones del hexágono y cálculo de vecinos
Cuando hablamos de las direcciones de un hexágono, nos referimos a las direcciones relativas de los lados de un hexágono respecto a su centro. La imagen siguiente representa las direcciones posibles para un hexágono dispuesto horizontalmente.
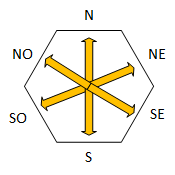
El uso de direcciones es fundamental para poder referirnos a los vecinos o hexágonos adyacentes. La obtención de vecinos es necesaria para diferentes diferentes cálculos y algoritmos, como la búsqueda de caminos (encontrar una ruta entre 2 celdas del mapa) y el cálculo de movimientos.
Dado un hexágono con coordenadas (i,j), se trata de calcular las coordenadas de los hexágonos adyacentes. Este cálculo va a depender de la dirección considerada. Por ejemplo, para calcular el vecino al NE de <0,0> hay que sumar 1 a la columna (i), y se obtiene <1,0>. Sin embargo, si queremos el vecino NE de <1,1>, y aplicamos la misma regla, obtenemos <2,1>, que no es correcto, pues en este caso habría que sumar 1 a la columna, pero también hay que restar 1 a la fila, y se obtendría <2,0>.
Si se estudia el sistema de coordenadas propuesto se observa que el cálculo de las coordenadas (i’, j’) de un hexágono adyacente a otro con coordenadas <i,j> en la dirección d, cumple lo siguiente:
- El cálculo de
i’depende únicamente ded - El cálculo de
j’depende dedy de siies par o impar.
Vamos a sintetizarlo en una tabla.
| Direction | incCol | incFilaPar | incFilaImpar |
|---|---|---|---|
| N | 0 | -1 | -1 |
| NE | 1 | 0 | -1 |
| SE | 1 | 1 | 0 |
| S | 0 | 1 | 1 |
| SO | -1 | 1 | 0 |
| NO | -1 | 0 | -1 |
| C | 0 | 0 | 0 |
La primera columna de la tabla es la dirección, la segunda el incremento que debemos aplicar a la columna (i), y la tercera y cuarta son los incrementos que debemos aplicar a la fila (j) dependiendo de si la columna es par o impar respectivamente.
Por conveniencia, se ha añadido una séptima dirección, que denominamos centro (C), y que apunta al mismo hexágono de referencia, es decir, que devuelve las coordenadas del mismo hexágono, y no un hexágono adyacente.
Con la estructura de datos definida en esa tabla es muy fácil describir las fórmulas para el cálculo de un vecino:
Dado un hexágono con coordenadas (i,j), las coordenadas (i’, j’) del hexágono adyacente en la dirección d, se calculan como:
i' = i + d->incCol
SI esPar('i)
ENTONCES j' = d->incFilaPar
SINO j' = d->incFilaImparConversión de píxeles a coordenadas hexagonales
En esta sección se explica como convertir la posición del puntero del ratón en unas coordenadas de mapa, es decir se describe la conversión de píxeles a coordenadas hexagonales.
Vamos a proceder en 2 pasos: dado un píxel
Obtención de coordenadas rectangulares, las cuales definirán un rectángulo dentro del espacio cubierto por nuestro mapa, dónde cae el píxel de interés. Obtención de coordenadas hexagonales mediante el cálculo de la zona exacta donde se encuentra el píxel respecto al área del hexágono. Obtención de coordenadas rectangulares
Se trata de calcular un rectángulo en el cual cae un píxel determinado de la imagen del mapa, a partir del cual obtendremos el hexágono. Para ello hay que aplicar una rejilla rectangular con tantos rectángulos como hexágonos. Si intentamos crear esa rejilla usando los rectángulos ADJG, veremos que se solapan entre sí.

El solapamiento implica que algunos píxeles pueden pertenecer a dos rectángulos a la vez, lo cual resulta un problema, pues necesitamos unas coordenadas únicas para cada píxel. La solución pasa por utilizar una rejilla diferente, tal y como se muestra a continuación:
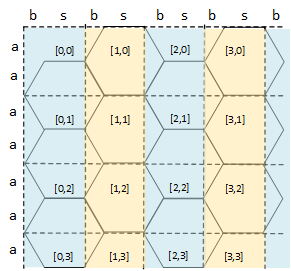
En vez de utilizar los rectángulos ADJG [con dimensiones w (anchura) y h (altura)], se utilizan rectángulos más pequeños, con la misma altura pero anchura b+s. Si nos fijamos veremos que ese tamaño se corresponde con el rectángulo ACIG.
Dado un píxel de coordenadas (x,y), calculamos las coordenadas (u,v) del rectángulo en el cual cae, según el sistema de coordenadas rectangular que acabamos de presentar, como sigue:
u = x / (b + s)
v = y / hSin embargo, esta nueva rejilla no se ajusta por igual a todos los hexágonos, sino que hay 2 casos posibles, marcados respectivamente en color azul y amarillo en la imagen anterior. La distinción entre un caso y otro es relevante para el cálculo de las coordenadas hexagonales, tal y como se describirá un par de secciones más adelante.
Obtención de las coordenadas hexagonales
Coordenadas relativas
Para calcular las coordenadas hexagonales, además de las coordenadas rectangulares (u,v) necesitamos obtener las coordenadas del píxel relativas al rectángulo (u,v), a las cuales denominaremos (rx, ry).
rx = x % (b + s)
ry = y % hCálculo de la pendiente
Para calcular las coordenadas hexagonales (i,j), hay que distinguir entre columnas pares e impares, y a partir de ahí determinar en qué hexágono está el píxel respecto del hexágono con coordenadas (u,v). Para lograrlo es preciso determinar en que zona cae el píxel dentro del hexágono.
El cálculo de las diferentes zonas de interés se basa en una magnitud: la pendiente p de la recta IF, la cual se computa como sigue
p = |JF| / |IJ|Si nos fijamos en la geometría del hexágono veremos que la longitud de JF es precisamente la apotema a, y la longitud de IJ es la magnitud b, así pues
p = a / bEsa pendiente nos va a permitir discernir si un píxel cae dentro o fuera de cierto hexágono, y más concretamente, en cuál de las 4 zonas exteriores posibles (ABE, CDF, EGH o IFJ). A partir de ese dato podremos calcular las coordenadas del hexágono en el cual está situado el píxel.
A continuación se describen los cálculos según si se trata de una columna par o impar.
Columnas impares
Para las columnas impares (en amarillo) hay 3 áreas distintas: el triángulo ABE, el triángulo EHG, y el resto del rectángulo (el polígono BCIHE). Dadas las coordenadas relativas (ur, vr), hay que considerar pues tres situaciones, caracterizadas por:
- Triángulo ABE: se cumple
ry < -p * rx+ a. Las coordenadas buscadas son las del hexágono al NO del hexágono con coordenadas(u,v). - Triángulo EHG: se cumple
ry > p * rx + a. Las coordenadas buscadas son las del hexágono al SO del hexágono con coordenadas(u,v). - El resto del rectángulo: no se cumple ninguna de las condiciones anteriores. Las coordenadas hexagonales son las mismas que las rectangulares.
Columnas pares
Para las columnas pares (en azul) hay 3 áreas distintas: la porción del hexágono por encima del segmento horizontal que divide 2 hexágonos, la porción del hexágono por debajo de ese segmento, y el triángulo a la izquierda.
- Triángulo a la izquierda: se cumple
ry > p * rx && ry < -p * rx + h. En este caso las coordenadas buscadas son las del hexágono al NO del hexágono con coordenadas(u,v). - Porción del hexágono por encima del segmento EF: se cumple
ry < a. En este caso las coordenadas buscadas son las del hexágono al N del hexágono con coordenadas(u,v) - Porción restante (hexágono por debajo del segmento EF): no se cumple ninguna de las condiciones anteriores. Las coordenadas hexagonales son las mismas que las rectangulares.
Calculo de las coordenadas de un hexágono adyacente
Una vez obtenida la dirección del hexágono vecino, el cálculo de las coordenadas se realiza según el procedimiento explicado más arriba (sección sobre las direcciones del hexágono).
i' = i + d->incCol
SI esPar(i')
ENTONCES j' = d->incFilaPar
SINO j' = d->incFilaImparImplementación en Java
A continuación se presenta una implementación básica de los conceptos anteriores que permite dibujar un mapa hexagonal e interaccionar con él mediante el ratón (pinchando sobre un hexágono se muestran las coordenadas del píxel apuntado y las coordenadas del hexágono correspondiente a ese píxel).
Como iremos viendo en este y otros artículos resulta muy práctico disponder de una clase Direction encargada de encapsular toda la información relativa a las direcciones de un hexágono. Una buena solución para implementar esta clase es el uso de Enum: cada dirección es una constante de tipo Enum<Direction> que tiene su propia información de estado y métodos asociados para obtener esa información.
public enum Direction {
N(0, -1, -1),
NE(1, 0, -1),
SE(1, 1, 0),
S(0, 1, 1),
SW(-1, 1, 0),
NW(-1, 0, -1),
C(0, 0, 0);
private final int incColumn;
private final int incRowEven;
private final int incRowOdd;
private Direction(final int incI, final int incJEven, final int incJOdd) {
this.incColumn = incI;
this.incRowEven = incJEven;
this.incRowOdd = incJOdd;
}
public int getIncColumn() {
return incColumn;
}
public int getIncRowEven() {
return incRowEven;
}
public int getIncRowOdd() {
return incRowOdd;
}
public Point getNeighborCoordinates(Point coordinates) {
int column = coordinates.x + getIncColumn();
int row = coordinates.y + (Util.isEven(coordinates.x) ? getIncRowEven() : getIncRowOdd());
return new Point(column, row);
}
}El método getNeighborCoordinates(Point coordinates) hace uso del método estático isEven(int number) para determinar si una coordenada es par o impar. Aunque determinar si un entero es par o impar es una tarea sencilla que no requiere más que una operación y una comparación, a efectos de legibilidad y mantenimiento del código es útil crearse unos métodos estáticos que se encarguen de hacer esa operación, y utilizarlos cuando sea necesario. En nuestro caso, hemos creado una clase dedicada a utilidades varias, que hemos denominado Util, y ahí hemos implementado esos métodos
public class Util {
public static boolean isEven(int number) {
return (number & 1) == 0;
}
public static boolean isOdd(int number) {
return (number & 1) == 1;
}
}A continuación describimos la clase HexagonalMap, la cual encapsula toda la información de un mapa y la representa gráficamente sobre un panel. Por simplicidad, de momento la misma clase HexagonalMap contiene la lógica del mapa y su representación gráfica.
Para la representación gráfica se utiliza (vía herencia) un JPanel. A nivel lógico se proporcionan los métodos tileToPixel y pixelToTile, encargados respectivamente de la conversión de coordenadas hexagonales a píxel y viceversa.
import javax.swing.*;
import java.awt.*;
public class HexagonalMap extends JPanel {
private int width; // Number of columns
private int height; // Number of rows
private int hexSide; // Side of the hexagon
private int hexOffset; // Distance from left horizontal vertex to vertical axis
private int hexApotheme; // Apotheme of the hexagon = radius of inscribed circumference
private int hexRectWidth; // Width of the circumscribed rectangle
private int hexRectHeight; // Height of the circumscribed rectangle
private int hexGridWidth; // hexOffset + hexSide (b + s)
public HexagonalMap(int width, int height, int hexSide) {
this.width = width;
this.height = height;
this.hexSide = hexSide;
hexApotheme = (int) (hexSide * Math.cos(Math.PI / 6));
hexOffset = (int) (hexSide * Math.sin(Math.PI / 6));
hexGridWidth = hexOffset + hexSide;
hexRectWidth = 2 * hexOffset + hexSide;
hexRectHeight = 2 * hexApotheme;
}
@Override
protected void paintComponent(Graphics g) {
super.paintComponent(g);
for (int i = 0; i < width; i++) {
for (int j = 0; j < height; j++) {
g.drawPolygon(buildHexagon(i, j));
}
}
}
@Override
public Dimension getPreferredSize() {
int panelWidth = width * hexGridWidth + hexOffset;
int panelHeight = height * hexRectHeight + hexApotheme + 1;
return new Dimension(panelWidth, panelHeight);
}
Polygon buildHexagon(int column, int row) {
Polygon hex = new Polygon();
Point origin = tileToPixel(column, row);
hex.addPoint(origin.x + hexOffset, origin.y);
hex.addPoint(origin.x + hexGridWidth, origin.y);
hex.addPoint(origin.x + hexRectWidth, origin.y + hexApotheme);
hex.addPoint(origin.x + hexGridWidth, origin.y + hexRectHeight);
hex.addPoint(origin.x + hexOffset, origin.y + hexRectHeight);
hex.addPoint(origin.x, origin.y + hexApotheme);
return hex;
}
Point tileToPixel(int column, int row) {
Point pixel = new Point();
pixel.x = hexGridWidth * column;
if (Util.isOdd(column)) pixel.y = hexRectHeight * row;
else pixel.y = hexRectHeight * row + hexApotheme;
return pixel;
}
Point pixelToTile(int x, int y) {
double hexRise = (double) hexApotheme / (double) hexOffset;
Point p = new Point(x / hexGridWidth, y / hexRectHeight);
Point r = new Point(x % hexGridWidth, y % hexRectHeight);
Direction direction;
if (Util.isOdd(p.x)) { //odd column
if (r.y < -hexRise * r.x + hexApotheme) {
direction = Direction.NW;
} else if (r.y > hexRise * r.x + hexApotheme) {
direction = Direction.SW;
} else {
direction = Direction.C;
}
} else { //even column
if (r.y > hexRise * r.x && r.y < -hexRise * r.x + hexRectHeight) {
direction = Direction.NW;
} else if (r.y < hexApotheme) {
direction = Direction.N;
} else direction = Direction.C;
}
return new Point(direction.getNeighborCoordinates(p));
}
public boolean tileIsWithinBoard(Point coordinates) {
int column = coordinates.x;
int row = coordinates.y;
return (column >= 0 && column < width) && (row >= 0 && row < height);
}
}Además, se incluye otro método, tileIsWithinBoard, que sirve para determinar si unas coordenadas hexagonales caen dentro del mapa o no (pues algunos píxels no quedan sobre ningún hexágono, sino en las zonas vacías que hay en los bordes superior e inferior del mapa)
Finalmente, la interfaz principal de la aplicación se ha implementando extendiendo un JFrame. Sobre la ventana principal se añade un panel de tipo HexagonalMap, y un panel de tipo MapInfo. El primero muestra el mapa hexagonal y el segundo la información relativa al puntero del ratón.
import javax.swing.*;
import java.awt.*;
import java.awt.event.MouseEvent;
import java.awt.event.MouseMotionAdapter;
public class HexagonalMapGUI extends JFrame {
static final int HEX_SIDE = 25; // side of hexagonal tile in pixels
static final int MAP_WIDTH = 10; // number of columns
static final int MAP_HEIGHT = 10; // number of rows
private HexagonalMap map;
private MapInfo info;
private JPanel mainPanel;
public HexagonalMapGUI() {
super("Hexagonal Map Demo");
info = new MapInfo();
map = new HexagonalMap(MAP_WIDTH, MAP_HEIGHT, HEX_SIDE);
map.addMouseMotionListener(new BoardMouseMotionListener());
mainPanel = new JPanel();
mainPanel.add(map);
mainPanel.add(info);
setContentPane(mainPanel);
}
public static void main(String[] args) {
java.awt.EventQueue.invokeLater(new Runnable() {
public void run() {
HexagonalMapGUI frame = new HexagonalMapGUI();
frame.setDefaultCloseOperation(WindowConstants.EXIT_ON_CLOSE);
frame.pack();
frame.setVisible(true);
}
});
}
private class BoardMouseMotionListener extends MouseMotionAdapter {
@Override
public void mouseMoved(MouseEvent me) {
info.setMousePosition(me.getX(), me.getY());
Point tileCoordinates = map.pixelToTile(me.getX(), me.getY());
if (map.tileIsWithinBoard(tileCoordinates)) {
info.setTileCoordinates(tileCoordinates);
} else info.setTileCoordinates(null);
}
}
}El resultado de ejecutar la clase anterior es el siguiente.
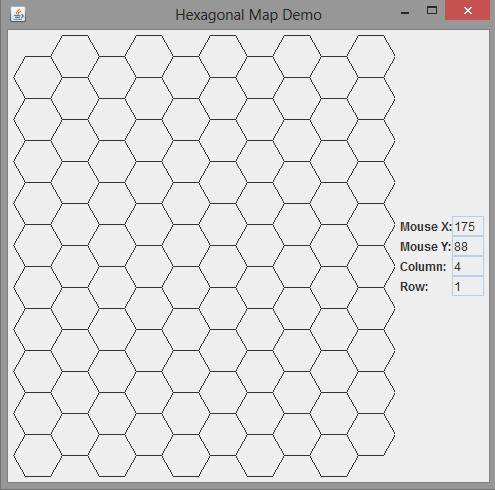
Si quieres, puedes clonar el proyecto tú mismo desde su repositorio en Github: HexagonalMaps.git
Puedes clonar o descargar el proyecto completo en GitHub. Lo que aquí se describe se corresponde con la versión 0.0.1.
Si quieres aprender técnicas para representar el terreno, ya está disponible el siguiente artículo: Mapas hexagonales (III): Representando el terreno.
Para saber más
- Sección en Red Blob Games.Esta Web, mantenida por Amit Pattel, es lo más completo que he encontrado en Internet sobre el tema, y está estupendamente realizada, si os interesa el tema y os defendéis con el inglés no os la podéis perder !
- Entrada sobre el hexágono en la Wikipedia, y entrada sobre teselados regulares.
- Entrada en la Wolfang MathWorld.
- Hexnet, Web dedicada al mundo de los hexágonos en general
- Esta página recoge varios enlaces de temática relacionada con los hexágonos